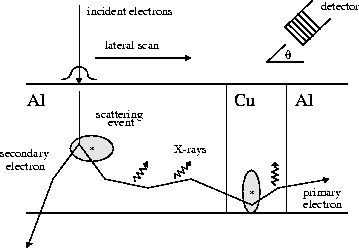
Monte Carlo trajectory simulation is an effective means of modeling high- resolution microscopes. I worked with Joe Michael and Al Romig from Sandia's materials center to create a parallel code for modeling beam/substrate interactions in an electron-beam microscope. We started with a serial code written by Dale Newbury and Bob Myklebust from NIST. The basic idea is shown in the following figure. Individual electron trajectories are tracked as they hit the surface and travel thru the substrate. Inelastic energy loss is computed as well as scattering events that may produce secondary electrons. The latter occurs in a random way via Monte Carlo rules. The trajectories of all the electrons are followed until they die out, transmit thru a thin-film sample, or backscatter from the incident surface. X-ray emission from primary and secondary electrons that would reach a detector is tallied along the way.

The obvious parallel algorithm for this model is to have each processor simulate one or more independent trajectories. For load-balancing we used a master-slave approach where each processor simulates a set of trajectories, then requests another set. A large parallel machine can rapidly accumulate good statistics for many millions of trajectories interacting with complex substrates. A bit of care must be taken to insure the random number stream used by each processor is truly independent. We experimented with several schemes for this which are discussed in the papers below.
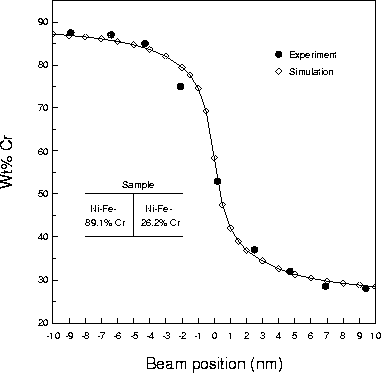
Here are some examples of how the Monte Carlo simulations can help calibrate or design microscopes and also be used to analyze experimental data. The scanning- electron micrograph is an Al thin film with 2% Cu. Some of the Cu has segragated to the Al grain boundaries (dark spots). The question is how sharply can these regions of Cu be resolved? Even if the interface between 2 materials is atomistically sharp, scanning the microscope beam across the interface will give a smeared-out profile due to beam spreading. The graph below shows a comparison between experiment and the Monte Carlo code for scanning a beam across a sharp interface between Ni-Fe-Cr alloys of different composition. In the simulation this "scanning" is done by simulating 100,000 or more electron trajectories at each of the data points shown. The excellent agreement between the 2 data sets is an example of how the simulation results can be used to deconvolve actual microscope data.

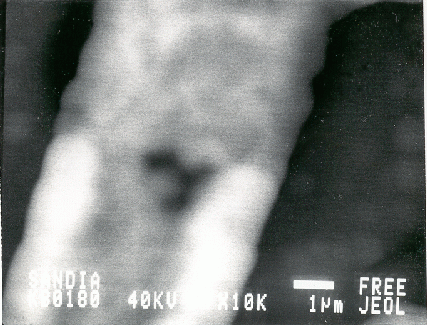
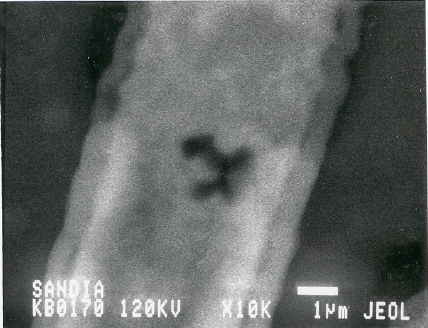
A large-scale calculation was also done of void imaging in Al metallization lines due to electromigration. These voids can be viewed in situ beneath an overlayer of passivation oxide if the beam voltage is within the proper range. The following 2 micrographs show the difference in void resolution with beam voltages of 40 KeV and 120 KeV.

The bottom 2 images are simulated pictures of a rectangular void beneath the same thickness of passivation at 40 KeV and 80 KeV. The actual void extent is shown as the rectangular box. This is an immense computation since many trajectories must be simulated at each pixel point in the 2-d image (actually only 1/4 of the pixels due to symmetry). We see the same kind of contrast dependence on beam voltage as in the actual microscope. These kinds of calculations can serve to optimize the contrast for a particular microscope as well as determine the ultimate resolution of what size voids can be "seen" thru a given passivation thickness.
Collaborators on this project:
The 1st of these papers focuses on the physics of the computational model and some interesting results. The 2nd has more discussion of the parallel issues along with parallel performance results. A discussion of the different techniques for parallel random number generation we tried is also included in the 2nd paper.
Parallel Simulation of Electron-Solid Interactions: A Rapid Aid for Electron- Microscope Data Interpretation, J. R. Michael, S. J. Plimpton, A. D. Romig Jr., Ultramicroscopy, 51, 160-167 (1993). (abstract)
Parallel Simulation of Electron-Solid Interactions for Electron-Microscopy Modeling, S. J. Plimpton, J. R. Michael, A. D. Romig, Jr., J of SuperComputing, 6, 139-151 (1992). (abstract)