NIMROD (non-ideal MHD with rotation - open discussion) is a multi-lab project sponsored by DOE's Office of Fusion Energy to create a new plasma simulation tool for tokamaks and alternates. This is the home page for the NIMROD project; it lists the team members and describes the code's physics equations, computational techniques, and some calculations performed to date.
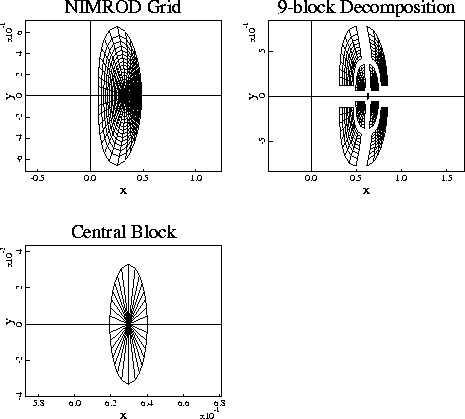
My contribution has been to the parallelization effort. NIMROD grids the poloidal plane of the tokamak with finite-element quads and triangles (in the center region or at the external boundary) as in the figure below. The toroidal direction is discretized with spectral modes. The decomposition of the 3- d domain to processors is done as a pre-processing step so that each processor owns one or more sub-blocks of elements and one or more of the modes associated with those elements.

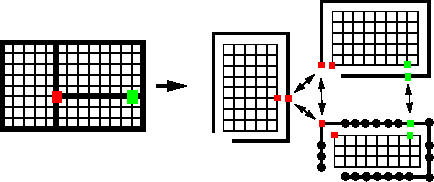
Interprocessor communication across the irregular sub-block boundaries occurs in the linear solver to fully form the matrix and right-hand side for each unknown and to perform matrix-vector multiplies. This so-called "seaming" procedure is shown pictorially in the figure below. Each sub-block adjoins other sub-blocks in an irregular fashion. A 1-d seam stores copies of the boundary values for each sub-block. Portions of each seam are exchanged with neighboring processors to fully sum the boundary values in each sub-block. For example, the green point is a summation on 2 procs; the red point is a summation across 3 procs. This seaming is done via message-passing using some efficient library routines I developed for irregular communcation. (See our grid transfer and PRONTO transient dynamics work for other applications of these ideas.) Additional communication across spectral modes is also done within NIMROD to perform on-processor 1-d FFTs within each finite element.
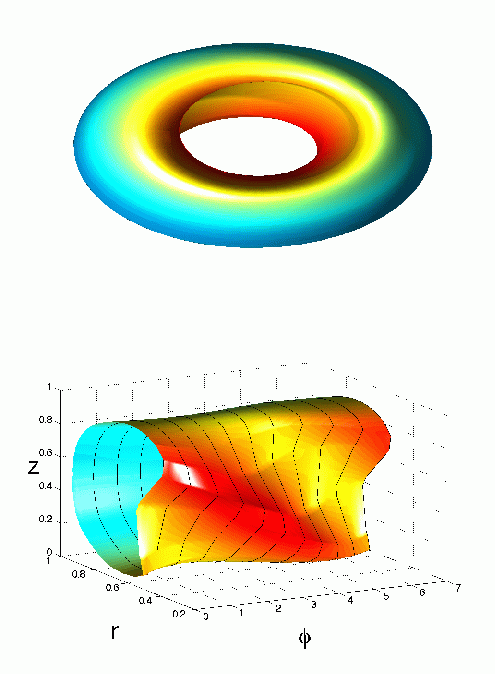
NIMROD is written in F90 with MPI calls. It runs portably on many machines; the biggest calculations to date have been run on the Cray T3E at NERSC. For large problems the code runs scalably on up to 256 processors of the T3E. A pretty picture of some tokamak modes is shown below; details are given on the NIMROD home page.
The linear algebra kernel within NIMROD is a conjugate gradient solver. Other team members have written several preconditioners for the solver, including Jacobi, line, and block-inversion preconditioners. Currently I'm working to integrate the AZTEC parallel linear solver package into NIMROD so we can experiment with 2-level multigrid and other preconditioning options.
Collaborators on this project:
These papers describe the equations and numerical algorithms used in NIMROD, as well as illustrate some simulation results.
The NIMROD Code: A New Approach to Numerical Plasma Physics, A. H. Glasser, C. R. Sovinec, R. A. Nebel, T. A. Gianakon, S. J. Plimpton, M. S. Chu, D. D. Schnack, and the NIMROD Team, Plasma Physics and Controlled Fusion, 41, A747- A755 (1999). (abstract)
Nonlinear Magnetohydrodynamics Simulation Using High-order Finite Elements, C. R. Sovinec, A. H. Glasser, T. A. Gianakon, D. C. Barnes, R. A. Nebel, S. E. Kruger, D. D. Schnack, S. J. Plimpton, A. Tarditi, and M. S. Chu, J Comp Phys, 195, 355-386 (2004). (abstract)