Particle-in-cell (PIC) codes solve Maxwell's equations for particles and fields on a grid. A team of researchers in the pulsed power group at Sandia has developed a relativistic electrodynamics PIC code called QuickSilver. QuickSilver grids are a concatenation of blocks; each block is a logically regular 3-d mesh with boundary conditions and internal structure such as conductors.

A timestep in QuickSilver consists of (1) advancing electric and magnetic fields on the grid via a finite difference approximation to Maxwell's equations, (2) creating, destroying, and pushing particles in reponse to Lorentz forces, and (3) computing the particle charge and current density contributions to the fields. We've created a parallel version of the code that's discussed in the report below. Parallelism is enabled by chopping each user-defined block into sub-blocks. Each processor is assigned one or more sub- blocks, and owns all the field values and particles in those blocks. The timestep then proceeds as in serial QuickSilver with a processor updating the field values and particles in its blocks. Communication is performed to update field values on block boundaries, and to migrate particles from one processor to another. For problems with a roughly uniform distribution of particles this works very well and we have run scalably (90% parallel efficiency or more) on 500-1000 processors of Sandia's large Intel Tflops machine. The real challenge in PIC codes is to load-balance both the grid and particle computations when particle densities vary dramatically in space and time. Our approach in QuickSiler is to balance the grid evenly across processors as a static pre-processing step. This insures that field updates will always be load-balanced. The particles are then dynamically load-balanced in the following way. On a timestep where particles become imbalanced, "windows" are created within a processor's block(s) that are overworked. Each window is assigned to a child processor that is underworked. For example, in the diagram below, if processor 1 has too many particles it creates 2 shaded window regions within its block, one for proc 0 and the other for proc 2.
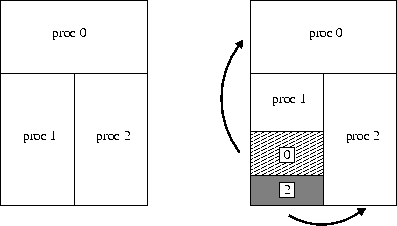
As particles move into the windows they migrate to the child processor; if they leave the window they migrate back to the parent. Field updates continue to be done by the parent. The windows persist until the particle distribution again becomes imbalanced, usually many timesteps later. This has the effect of load- balancing the particles independently of the field updates, at the cost of extra particle migration and field communication. If particles dominate the overall computation, as is often the case, this is a good trade-off. We've tested this approach on problems with both static and dynamic imbalance. On the Tflops machine, QuickSilver typically stays within a factor of 2 (or better) of perfect speed-up even when the load-imbalance is a factor of 10x or more.
Collaborators on this project:
Details of our QuickSilver parallelization and load-balancing techniques as well as several tables of parallel performance are given in this paper:
A Load-Balancing Algorithm for a Parallel Electromagnetic Particle-in-Cell Code, S. J. Plimpton, D. B. Seidel, M. F. Pasik, R. S. Coats, G. R. Montry, Comp Phys Comm, 152, 227-241 (2003). (abstract)
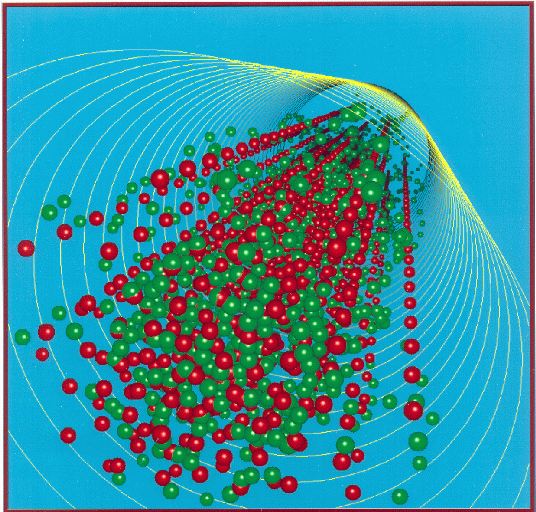
I also worked on an older electromagnetics particle code called Buckshot, which models the interactions in an emitted beam of positive- and negative-charged particles. Though not technically a PIC code, it did present interesting parallelization challenges, particularly for load-balancing as the beam grew from zero-size initially to a large length. As shown below, it also produced some pretty cool pictures!
Collaborators on this project:
Here's a conference paper on this work:
Load Balancing and Performance of a Gridless Particle Simulation on MIMD, SIMD, and Vector Supercomputers, S. J. Plimpton, I. Shokair, J. Wagner, in Proc of 5th SIAM Conference on Parallel Processing for Scientific Computing, Houston, TX, March 1991, p 507-512. (abstract)